How Do You Know if Its Nonremovable or Removable

mars 14, 2022 Enregistrer un commentaire

What Is Removable Discontinuity?
- How do you solve a removable discontinuity?
- What is the divergence betwixt a removable and non removable discontinuity?
- Non Removable Discontinuity\Removable And Nonremovable Discontinuity
- What Is A Removable Discontinuity
- Give An Example Of A Function With Both A Removable And A Not-removable Discontinuity

What Is Removable Discontinuity?

Removable Discontinuity: Aremovable aperture is a point on the graph that is undefined or does not fit the rest of the graph. There is a gap at that location when you are looking at the graph. When graphed, a removable discontinuity is marked by an open up circumvolve on the graph at the point where the graph is undefined or is a different value similar this.

In that location are two means a removable aperture can exist created. Allow'south talk about the commencement i now. Do you run across it? There is a small open up circumvolve at the point where x=2.v approximately.

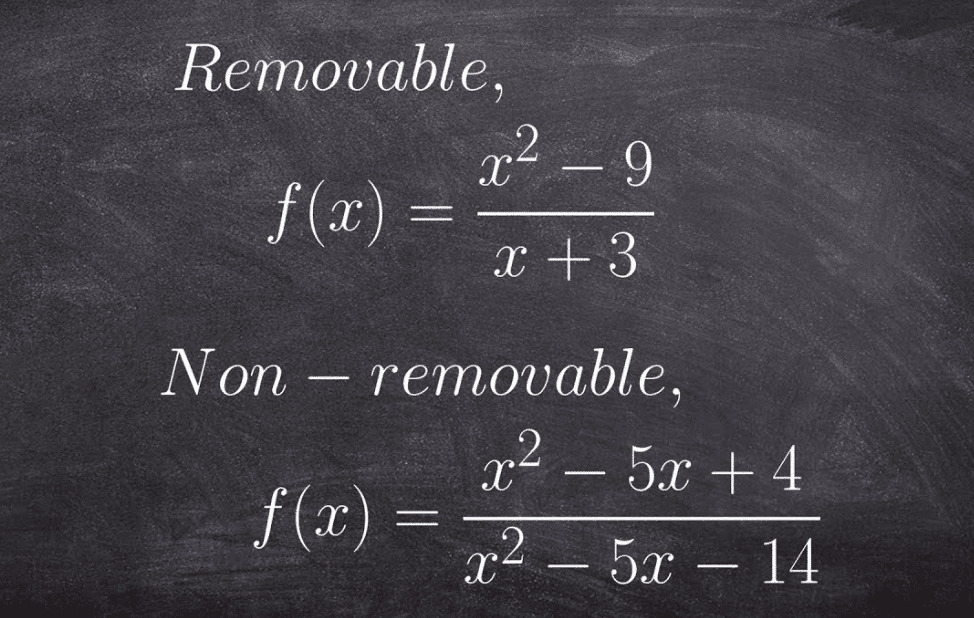
A pigsty in a graph. That is, a discontinuity that can be "repaired" by filling in a single signal. In other words, a removable discontinuity is a bespeak at which a graph is not connected just tin can be made continued by filling in a single point.

Read Also: Parent Functions And Transformations

Formally, a removable discontinuity is one at which the limit of the part exists but does not equal the value of the function at that bespeak; this may be considering the function does not exist at that point.

Removable Discontinuities, cont.

Footstep 1: Factor the numerator and the denominator.
Stride ii: Identify factors that occur in both the numerator and the denominator.
Pace 3: Fix the common factors equal to zero.

Pace 4: Solve for x.

[Calculus 1]What is the departure betwixt a removable and not removable discontinuity? … If the limit doesnot exist, then thediscontinuity isnon–removable.In essence, if adjusting the function'southward value solely at the bespeakof discontinuity will return the function continuous, and then thediscontinuity isremovable.

Non Removable Discontinuity\Removable And Nonremovable Discontinuity

As your pre-calculus teacher volition tell you, functions that aren't continuous at anx value either accept aremovable discontinuity (a pigsty in the graph of the role) or anonremovablediscontinuity(such as a leap or an asymptote in the graph):

If the function factors and the bottom term cancels, the discontinuity at thex-value for which the denominator was zero is removable, so the graph has a hole in it.

For example, this function factors as shown:

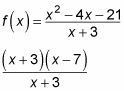
After canceling, information technology leaves you withx – 7. Thereforex + three = 0 (orx = –iii) is a removable discontinuity — the graph has a hole, like you see in Figure a.

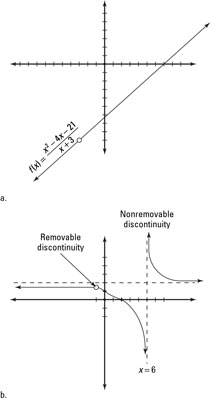
The graph of removable leaves you feeling empty, whereas a graph of a not-removable discontinuity leaves yous feeling jumpy.
If a term doesn't cancel, the discontinuity at thisx value corresponding to this term for which the denominator is zero is nonremovable, and the graph has a vertical asymptote.

The following function factors as shown:

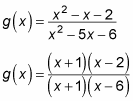
Because the10 + 1 cancels, you accept a removable at10 = –1 (you'd come across a hole in the graph there, not an asymptote). But thex – 6 didn't cancel in the denominator, and then you accept a nonremovable discontinuity atx = 6. This aperture creates a vertical asymptote in the graph atx = six. Figure b shows the graph of1000(x).

What Is A Removable Discontinuity

A removable discontinuity can be created past defining a bleep in the graph like this.

Defining a bleep.

The in a higher place function tells us that the graph generally follows the function f(x)=x^2-one except for at the point ten=4. When we graph information technology, we volition need to draw a piffling open circle at the point on the graph and marker that it equals 2 at that point. This is a created discontinuity. If you were the 1 defining the office, you can easily remove the discontinuity by redefining the part. Looking at the function f(x)=x^2-1, nosotros can calculate that at x=4, f(x)=xv. So, if we redefine our indicate at x=4 to equal xv, nosotros volition have removed our

removable discontinuity

If we were to graph the above, nosotros would get a continuous graph without any discontinuities. When yous meet functions written out similar that, exist sure to check whether the function really has a discontinuity or non. Sometimes the part is continuous only simply written like it isn't just to be tricky.

Give An Example Of A Part With Both A Removable And A Non-removable Discontinuity

A real-valued univariate function is said to have a removable discontinuity at a betoken in its domain provided that both and

(1)

be while. Removable discontinuities are so named because i can "remove" this point of discontinuity by defining an most everywhere identical function of the form

$F(x)={f(x) for x!=x_0; L for x=x_0,$

(2)

which necessarily is everywhere-continuous.

RemovableDiscontinuity

The figure above shows the piecewise function

$f(x)={(x^2-1)/(x-1) for x!=1; 5/2 for x=1,$

(3)

a function for which while. In particular, has a removable discontinuity at due to the fact that defining a office as discussed higher up and satisfying would yield an everywhere-continuous version of.

Notation that the given definition of removable discontinuity fails to apply to functions for which and for which fails to exist; in particular, the above definition allows one only to talk about a role being discontinuous at points for which it is defined. This definition isn't uniform, however, and as a result, some authors claim that, e.g., has a removable aperture at the point. This notion is related to the so-called sinc function.